小問#1 領域を塗りつぶすブラシ半径の最大は？

問題

半径 $a \: (>0)$ のブラシで領域 $y \geq x^2$ をすべて塗りつぶすための $a$ の条件を求めよ．

???

ブラシが境界線の外にはみ出てはいけないということである．はみ出ないぎりぎりのところはブラシと領域の関係がどうなっているのかを考えたい．

解答

問題文は「ブラシが領域に含まれるブラシ半径 $a$ の条件」と言い換えられる．領域の境界線は下に凸の (陽) 関数であるため，境界線をすべて塗れたならば，そのブラシで境界線より内部をいくらでも塗ることができる．よって，境界線に接するブラシが領域に含まれる条件を考える．以下，この解答ではブラシを円と呼ぶ．
中心 $\rm{O}_1$ が領域内部にあり，境界線上の点 $\rm{T} $${(t,t^2)}$ で接している円 $C$ を考える．点 $\rm{T} $ ははみ出さず塗ることができるが，例えば点 $\rm{T} $ 以外のところで少しでも円が領域外に出ていると，境界線をはみ出して塗ることになり題意を満たさない．

ここでは，円が領域に含まれるかどうかを，円 $C$ の中心 $\rm{O}_1$ の位置条件ごとにまとめた．

$\rm{O}_1$ が $y$ 軸を挟んで点 $\rm{T}$ と反対側にある ⇒ 円の一部が領域外
境界線 $y = x^2$ が $y$ 軸対称であるため，円 $C$ は放物線と交点を持つ．
$\rm{O}_1$ が $y$ 軸上にあるとき ⇒ 円の全部分が領域内
対称性により点 $\rm{T}$ の $y$ 軸対称の点 $(-t,t^2)$ でもう一つの接点を持つ．
円と二次関数の共有点を求める方程式の次数が高々4であるため，二つの接点 (接点は重解) 以外に共有点を持たない．
$\rm{O}_1$ が $y$ 軸を挟んで点 $\rm{T}$ と同じ側にあるとき ⇒ 円の全部分が領域内
上の2で考えた円に完全に含まれるため，点 $\rm{T}$ 以外に共有点を持たない．

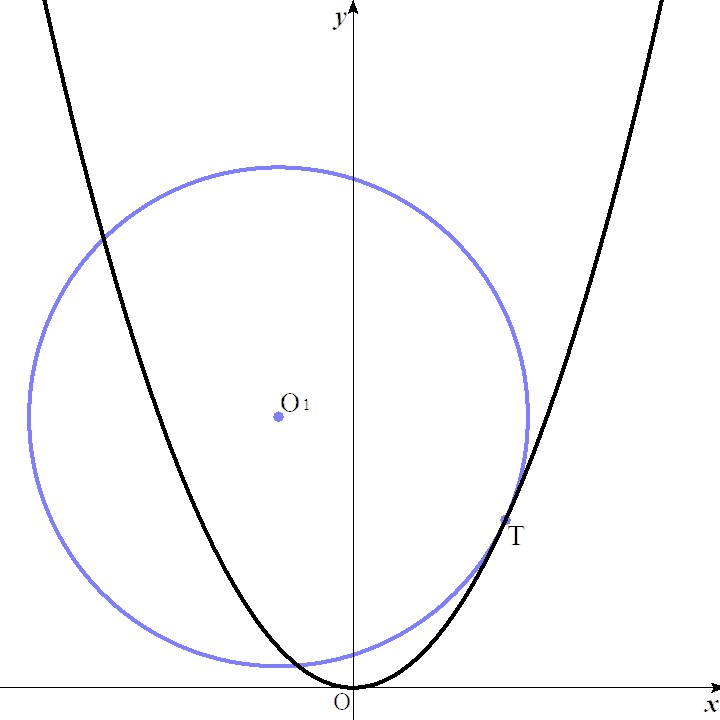
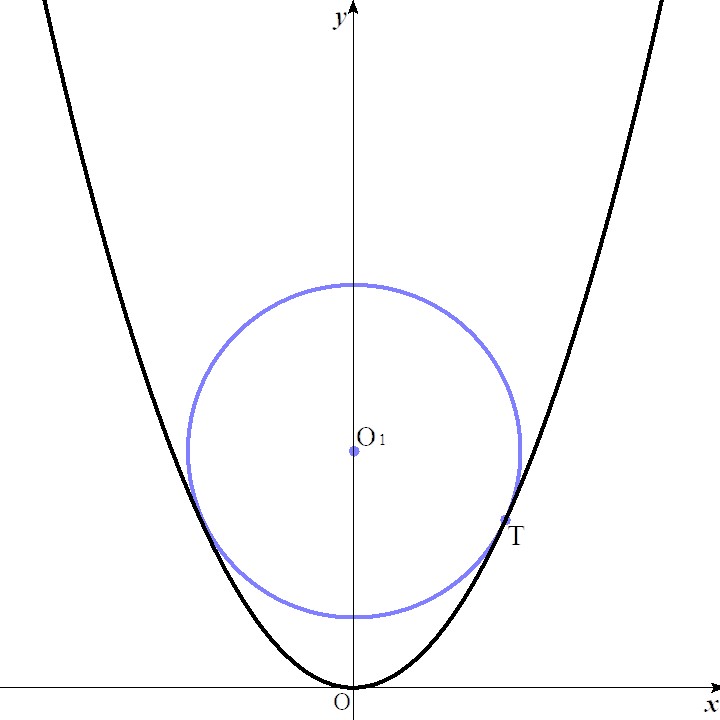
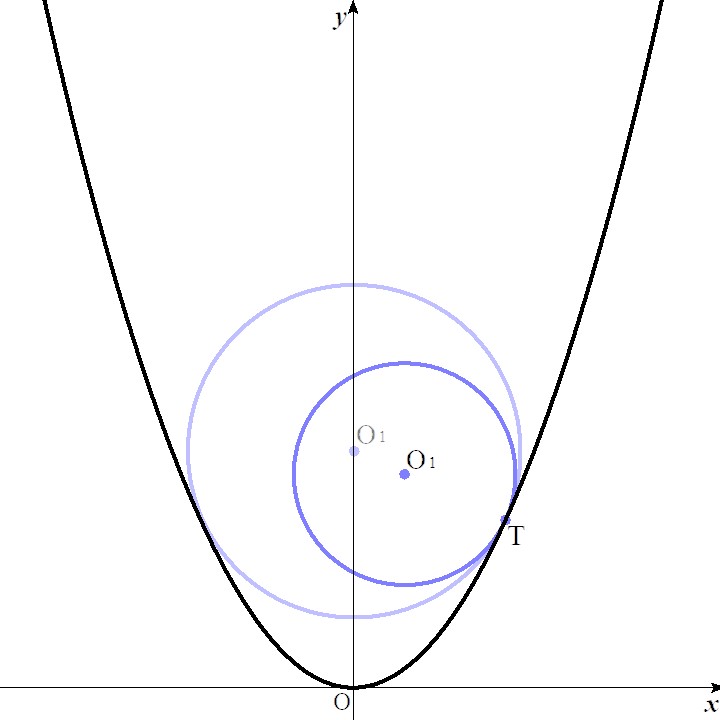
図1 $\rm{O}_1$ が $y$ 軸を挟んで
点 $\rm{T}$ と反対側にある場合

図2 $\rm{O}_1$ が $y$ 軸上にある場合

図3 $\rm{O}_1$ が $y$ 軸を挟んで
点 $\rm{T}$ と同じ側にある場合

以上より，円 $C$ の全部分が領域内に収まる条件は，$\rm{O}_1$ が領域内部で，かつ， $y$ 軸上か， $y$ 軸を挟んで点 $\rm{T}$ と同じ側にあることと分かった．また， $\rm{O}_1$ が $y$ 軸上にある場合が，ある点 $\rm{T}$ を塗ることのできる $a$ の範囲の最大となることも図3より明らかである．これを任意の点 $\rm{T}$ において $a$ の範囲の共通部分を求めると答えとなる．

$\rm{O}_1$ は点 $\rm{T}$ における法線ベクトル $\vec{n} = (\frac{-2t}{\sqrt{1+4t^2}},\frac{1}{\sqrt{1+4t^2}})$ を用いて，$$\rm{O}_1 \: (t-\frac{2at}{\sqrt{1+4t^2}},t^2+\frac{a}{\sqrt{1+4t^2}})$$ と表される． $\rm{O}_1$ が $x$ 軸にあるかそれより点 $\rm{T}$ に近いときは，$(t-\frac{2at}{\sqrt{1+4t^2}})\times t \geq 0$ であるため，これを解くと，$a \leq \frac{\sqrt{1+4t^2}}{2}$となり，任意の $t$ での $a$ の共通部分と問の条件から，答えは $0 < a \leq 1/2$ である．