2022年，カタールワールドカップ．サムライブルーが私たちに勇気と感動を与えてくれた．「死の組」と呼ばれたグループリーグでドイツとスペインを破ったのだ．総勝ち点6，死闘を制しグループ首位で決勝トーナメントへ駒を進め，初戦のクロアチアとPKまでもつれ込んだが惜しくも破れてしまった．他チームの試合結果によっては敗退する可能性があったために，ひやひやしながらの応援を余儀なくされていた．なぜ，勝ち点6でも敗退する可能性があるのか？では何点であれば「他チーム同士の試合結果に依らず，グループリーグを自力で突破できるのか？」
導入
グループリーグの突破チームを決める方法
W杯のグループリーグは4チームが総当たりで戦う．勝つと3点，引き分けると1点，負けると0点がもらえ(これらを勝ち点と呼ぶ)，最終的に総勝ち点の高い2チームがグループリーグを突破し決勝トーナメントに出場できる．当落線上に2チーム以上いた場合，得失点差→得点→直接対決の勝敗→フェアプレーポイントの順に，優劣のつくまで比較する．
ギモンの言い換えと解き方の提示
突破を『自力』で決めるということは，「他チーム同士の試合結果がどうであれ，自チームより総勝ち点の低いチームが2つ以上ある」と言い換えられる．例えば，自チームが9点だとすると，3勝しているから他チームが6点以下と決まる．これは，自チームより低いチームが2つ以上あるため命題が成立する．では次は7点で思考実験をしてみよう．．．と思ったが，具体的に9点，7点，…と当てはめてやっている人はすでにいるので，先輩方に解説をお任せして，この記事では (面白いかなと思い) 総勝ち点を文字において導くことにした．
解いてみる
命題を満たす条件を式にする
自チーム \(\rm{O}\) の総勝ち点を \(W_o ( \geq 0)\) ，残り3チーム \((\rm{A}，\rm{B}，\rm{C})\) の総勝ち点をそれぞれ \(W_a, W_b, W_c ( \geq 0)\) とする． 対称性より， \(W_a \geq W_b \geq W_c \) として構わない．ここで，中位(ここでのチーム \(\rm{B}\) )がこの問題の鍵を握る．命題が成り立つには， \(\rm{B}\) の取りえる最大の総勝ち点 \(W_{b, max}\) を \(W_o\) が上回っていなければならない． \(\rm{B}\) は \(W_{b, max}\) 点以上に良くならないため， \(W_o\) がより大きければ必ず命題が成立するということだ．式にすると，
\begin{equation}W_o > W_{b, max}\end{equation}
となる．
チームの総勝ち点から式を解く
方針がわかったところで，\(\rm{O}\) の勝利数を \(w\) ，引き分け数を \(d\) と置いて命題が成り立つのに必要な \((w, d \in \mathbb{N})\) の範囲を評価しよう．まずは \((w, d)\) を用いて \(W_o\) を表すと，
\begin{equation}W_o=3w+d\end{equation}
となる．ただし， \(w+d \leq 3 (w, d \in \mathbb{N})\) である．残り3チームの合計総勝ち点は分かるだろうか？3チーム同士の試合結果によって合計点が変わってくるため，具体的に何点かははっきりとわからないが，何点以下かは \(\rm{O}\) の総勝ち点で分かる．このリーグの試合数は6であり，1試合ごとに勝負ありだと3点が，引き分けだと2点が試合をしたチームに配分される．すべての試合が勝敗ありだと全チームの合計総勝ち点は18となり，1試合引き分けが生じるごとに17，16．．．と1点ずつ減少する． \(\rm{O}\) の総勝ち点は \((3w+d)\) 点であり，引き分けは \(d\) 試合あったため，残り3チームの合計総勝ち点は，
\begin{equation}W_a + W_b + W_c \leq 18-d-(3w+d)\end{equation}
となる．
次に，\(W_{b, max}\) (中位チーム (チーム \(\rm{B}\) ) の最大総勝ち点) を \((w, d)\) を用いて表そう．\(W_b\) を最大化するためには，逆に他2チームがとりえる最小値を考えて，合計から引けばよい．この場合は，\(W_a = W_b, W_c = 0\) であるから，上の不等式に代入すれば，
\begin{equation}W_{b, max} \leq \frac{18-3w-2d}{2}\end{equation}
となる．
最後に，命題の式に代入する．
\begin{align}
3w+d &> \frac{18-3w-2d}{2} \\
d &> -\frac{9}{4}(w-2)
\end{align}
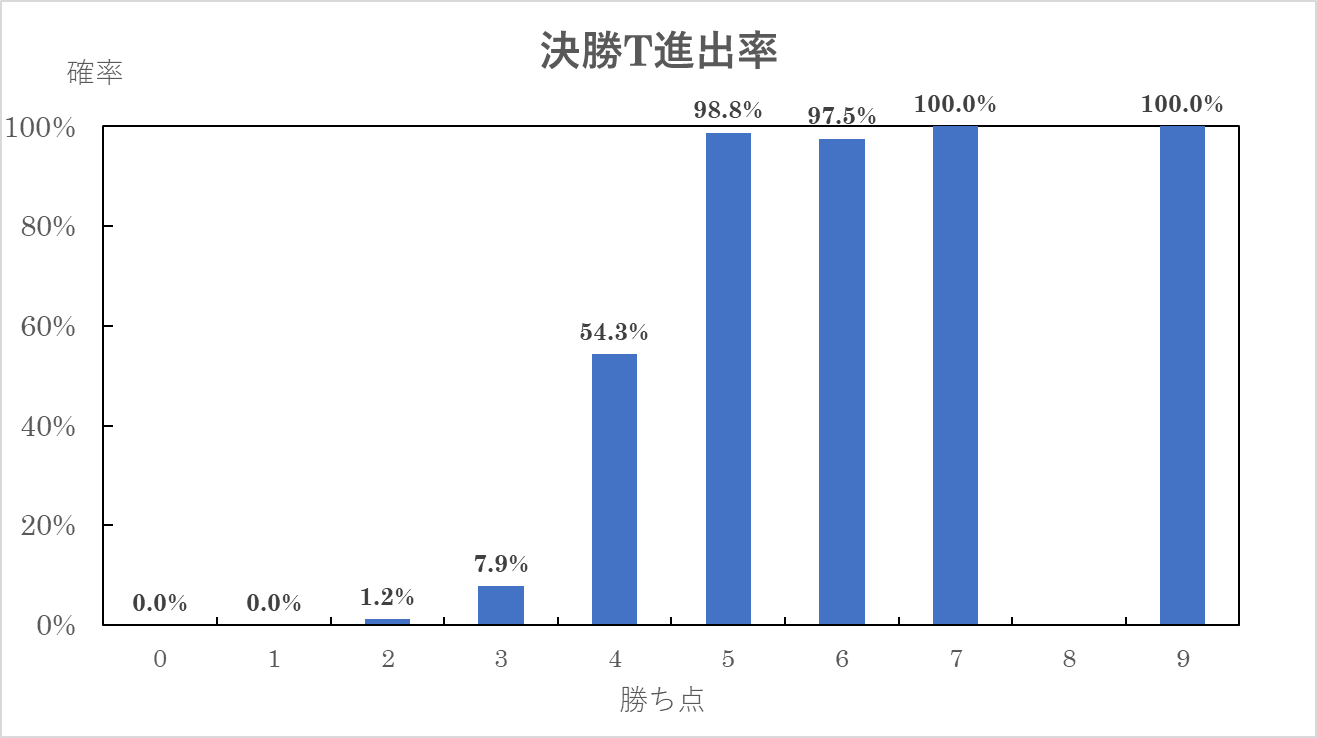
これを満たすのは， \((w, d)=(2, 1), (3, 0)\) しかなく，命題を必ず満たす勝ち点は \(7, 9\) 点となる．つまり， \(7, 9\) 点ならば十分に命題を満たすため，これは十分条件である．
よって，これで6点以下が必ず命題が成り立たないと示されたわけではないことに注意されたい．6点以下で \(W_{b, max} \geq W_o\) になる組があるかどうかを調べなければならない．
コメント